Improvements in Thermal Performance of Mango Hot-water Treatment Equipments: Data Analysis, Mathematical Modelling and Numerical-computational Simulation

Mendoza Orbegoso, Elder M.; Villar-Yacila, Paul; Marcelo, Daniel; Oquelis, Justo

DOWNLOAD FULL TEXT PDF

Original scientific paper

Journal of Sustainable Development of Energy, Water and Environment Systems
Volume 5, Issue 2, June 2017, pp 219-239
DOI: https://doi.org/10.13044/j.sdewes.d5.0145

Elder M. Mendoza Orbegoso , Paul Villar-Yacila, Daniel Marcelo, Justo Oquelis

Mechanical-Electric Engineering Department, University of Piura, Av. Ramón Mugica 131, Urb. San Eduardo, Piura, Perú

Abstract

Mango is one of the most popular and best paid tropical fruits in worldwide markets, its exportation is regulated within a phytosanitary quality control for killing the “fruit fly”. Thus, mangoes must be subject to hot-water treatment process that involves their immersion in hot water over a period of time. In this work, field measurements, analytical and simulation studies are developed on available hot-water treatment equipment called “Original” that only complies with United States phytosanitary protocols. These approaches are made to characterize the fluid-dynamic and thermal behaviours that occur during the mangoes’ hot-water treatment process. Then, analytical model and Computational fluid dynamics simulations are developed for designing new hot-water treatment equipment called “Hybrid” that simultaneously meets with both United States and Japan phytosanitary certifications. Comparisons of analytical results with data field measurements demonstrate that “Hybrid” equipment offers a better fluid-dynamic and thermal performance than “Original” ones.

Keywords: Mangoes, Hot-water treatment, 0-D mathematical modelling, Computational fluid dynamics, Pipe-type heat exchanger, Heat transfer efficiency.

Views (in 2025): 388 | Downloads (in 2025): 107
Total views: 6433 | Total downloads: 4107

INTRODUCTION

The mango (Mangifera Indica L.) is one of the most important tropical fruit because it represents almost 50% of all tropical fruits produced worldwide [1] and which global production overcomes 26 tons annually [2]. This fruit is one of the flagship products of Peru and its production is mainly concentrated in the coastal valleys of the northern region that covers 68-72% of the total Peruvian production of mango [3] and comprises approximately 17,000 hectares [4]. This tropical fruit is one of the most appreciated, popular and fetches the highest prices in international markets such USA, Europe and Asian countries.

In order to be exported, the mango must pass to a phytosanitary control for the purpose of eliminating the “fruit fly”, especially the Ceratitis Capitata, which is one of the most harmful plagues in the world because, it attacks over 250 vegetables and fruit plants. In Peru, the “fruit fly” is one of the plagues most feared by farmers causing losses up to 100 million dollars [5], as it is capable of ruining mango crops and creating phytosanitary barriers for its exportation.

If the mango is to be exported to other countries, it must undergo to different processes in order to comply with phytosanitary protocols that each importing country demands. Before the 80’s decade, mangoes intended for exportation were submitted to fumigation with ethylene dibromide before exportation. However, in 1986, the Environmental Protection Agency (EPA) announced the ethylene dibromide would be deregulated for use of all fruit intended for human consumption in the United States [6]. Later, world-wide countries also were concerned about ethylene dibromide as chemical treatment prior to fruit exportation. So, this chemical was banned for their use while alternative physical processes as hot-water treatment were allowed in order to eradicate the “fruit fly” plague.

This hot-water treatment is the process widely used by Peruvian agro-industrial companies and consists in the mango immersion in hot water at a certain temperature for a period of time that depends of the specific phytosanitary protocol demanded by each importing country [7]. The temperature for which the mango is subjected must be controlled and recorded in a way that it meets the required certification standards for each fruit importing country. If mangoes are to be exported to USA and Japan countries, Peruvian agro-industrial companies need to adopt new technologies in order to meet with the stringent exporting protocols that the aforementioned countries have been established.

At present, some agro-industrial companies in northern Peru have mango hot-water treatment equipments, here called as “Original”. These equipments meet the stringent phytosanitary requirements for the product to be exported only to the USA markets [8]. Although those “Original” equipments were designed according to good engineering practices, it has not a scientific-technological basis to ensure an optimum performance. In particular, it is assumed that such equipments are not thermally efficient. In addition, they have the difficulty in complying with the phytosanitary protocols required by Japan for the mango exportation.

Objective

In order to solve existing issues in “Original” equipments, it is imperative to apply constructional and operational improvements that permit to obtain a better use of thermal resources while meeting the American and Japanese standards required for the exporting of mango to these countries.

If constructional improvements of the “Original” equipment are to be applied, it is fundamental to identify its actual performance during the hot-water treatment process. This involves the development of a preliminary mathematical model to reproduce the transient behaviour of the thermal energy transport from the tank water to immersed mangoes.

In this work, analytical, experimental and computational numerical simulation studies are developed in order to determine the current thermal behaviour of the “Original” equipment. This equipment is the starting point for its design modifications in order to enhance the thermal performance at the same time satisfying the strict regulations imposed by USA and Japan countries for the export of mangoes to those countries. The resulting improved equipment shall be called as “Hybrid” because this unit will be able to meet with both USA and Japan phytosanitary requirements for the mango exportation to those countries.

Bibliographical review

Over the last two decades, several phytosanitary studies concerning the determination of the mortality rate of fruit fly larvae and eggs inoculated in fleshy fruits were carried out. For the mango case subjected to hot-water treatment, Sharp and Picho-Martinez [5] studied experimentally the mortality rate of three fruit fly larvae (Ceratitis Capitata, Anastrepha Obliqua, Anastrepha Distincta and Anastrepha Fraterculus) of two kind of mid-sized Peruvian mangos (Haden and Kent) submersed to water at 46.1 °C constant temperature. In this study, averaged times of 76.1, 113.4, 65.8 and 75.6 min ensured the death of 100% Ceratitis Capitata, Anastrepha Obliqua, Anastrepha Distincta and Anastrepha Fraterculus larvae population, respectively. An analogous study also was carried out by Nascimento et al. [9] where Brazilian mangoes (Atkins, Haden and Keith) were exposed to 45.9 and 46.3 °C hot-water in order to kill eggs and larvae of (Ceratitis Capitata, Anastrepha Obliqua and Anastrepha Fraterculus). Averaged times of 59.4 and 79.7 min guaranteed the 100% death of Ceratitis Capitata eggs and larvae. While 65.7 and 65.2 min of mangoes exposed to hot-water were necessary for the death of all Anastrepha Obliqua eggs and larvae. The minimum times 39.7 and 68.5 min were taken into account for the kill of the respective Anastrepha Fraterculus eggs and larvae.

In the modelling-simulation approach, there are very few research works devoted to the characterization of the transient heating of fruits during hot-water treatment. Wang et al. [10] developed a mathematical model with the purpose of studying the heat transfer rate for several fleshy fruits that are influenced by the heating medium speed as well as their thermal properties and size. The results demonstrated that the size of the fruit is the most important parameter in the heating rate whilst fruit thermal conductivity has a little effect in the transient behaviour of heating process. Experimental and Computational Fluid Dynamics (CFD) modelling studies were carried out by Rezagah et al. [11] in order to describe the transient heat transfer of three several kinds of Japanese pears during tempering. In this study, a 3-D laser scanner was utilized for obtain a 3-D geometry of a pear whereas T type copper-constantan thermocouples were used in order to monitoring the transient temperatures inside the peers during heating. The numerical results showed an excellent concordance with the experimental ones, validating the predictive capacity that CFD modelling offers in the describing of the transient conduction heat transfer of fruits during heating. Experimental, modelling and simulation approaches was performed by Valle-Guadarrama [12] with the purpose of estimating the thermal diffusivity, the convective heat transfer coefficient and the heating/cooling rates of Mexican lime during quarantine hot-water and hot-air treatments. In that study, it also was determined a maximum critical flow velocity where the heating/cooling rates are no changed with a subsequent increase of the flow velocity and this critical parameter is reduced as the fruit size grows. To the best of the authors’ knowledge, there is not any research work that attempts to study the fluid dynamics and thermal transport of an industrial hot-water treatment equipments in order to efficiently meet with the phytosanitary requirements claimed by importing countries.

Description of mango’s hot-water treatment equipments

As is shown in Figure 1, hot-water treatment equipments for the mango quarantine process, consists of:

A high capacity tank containing hot water above 46.1 °C (115 °F);
Pipe’s type heat exchanger, where steam flows inside the pipe transfers thermal energy to the tank-water;
Propellers that generate the flow required to speed up the heat transfer process;
A dividing wall that separates the tank in regions where:
Pipe heat exchangers warm the tank-water;
Mangoes are immersed;

Controlling and monitoring systems, which control the on-off steam flow through the pipe heat exchanger according to the tank-water temperature;

Power systems, in which marine propellers are driven by induction motors.

Figure 1.

Mango hot-water treatment equipment - this configuration is related to the “Original” equipment

Phytosanitary procedures for the mango exportation to USA

With the purpose of eliminate the fruit fly; it is imperative that mangoes must be submitted to a hot-water treatment. This process consists in submerging the mangoes into hot water at a certain temperature and for a specific period of time that comprises between 75 and 90 minutes, depending the mango weight and its type. The water temperature must be controlled and recorded so that it remains within a strict margin for most of the time of the process.

For a proper hot water treatment of the mango, it should meet a certain number of procedures that are required by the standards of each importing country. For the USA hot-water treatment, it must fulfil the following main requirements [8]:

Mangoes should be immersed; at least 10 cm deep, during the period of time the hot-water treatment lasts;
During the hot-water treatment, mangoes cannot be immersed less than 75 min neither more than 90 min;
At the start of the treatment, the minimum temperature of mango mesocarp must not be less than 21.1 °C (70 °F);
The tank water must flow continuously in order to maintain its temperature above of 46.1 °C (115 °F) during the period of time the hot-water treatment lasts;
The water temperature sensors must be closely monitored within the first 5 minutes of the hot-water treatment. It is required that these temperatures exceed 46.1 °C (115 °F) within the first 5 minutes. If that is not the case, the treatment must be repeated using a slightly higher “control point” temperature;
During the commercial treatment, temperature differential of the tank water measured by permanent sensors located in different positions of the tank must not exceed 1 °C (1.8 °F).

MATERIALS AND METHODS

Three solution approaches is described in this section with the purpose of improving the thermal performance of the current “Original” hot water treatment equipment.

Field data acquisition of “Original” equipment

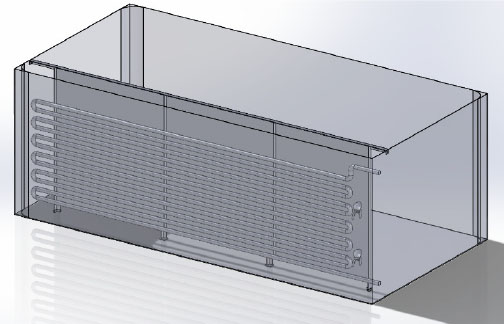
Figure 2 shows the geometrical configuration of mango hot-water treatment equipment that currently Peruvian agro-industrial companies use for the mango exportation to the USA. This equipment is referred as “Original” equipment.

Figure 2.

3-D configuration of the “Original” equipment that is currently used by Peruvian agro-industrial companies for the hot-water treatment of mango

Using the “Original” equipment shown by Figure 2, for different positions in the tank, Malca [13] obtained water temperature recordings over 90 minutes that the hot water treatment lasted. The left hand side of Figure 3 shows the conditioning of 1 of 12 RTDs (Pt 100) that were placed at different locations of the tank in order to record the transient behaviour of water temperatures. The right side of Figure 3 displays, as an example, a graph of the recorded temperature given by 1 RTD. It can be seen that in the first 26 min after immersing the mangoes, there is a sudden drop in the water temperature of the tank water resulting from an intense energy transfer from the water to the mango.

Figure 3.

Positioning of 1 RTD (PT 100) in a plastic basket filled by mangoes and temperature recording obtained by the sensor

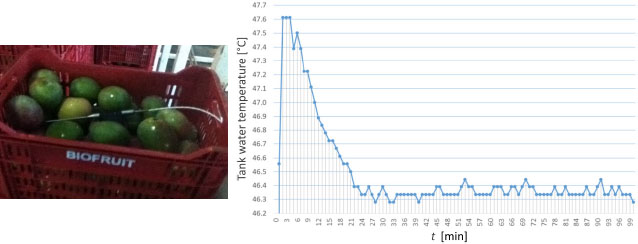
This sudden water cooling process continues until it reaches a pre-established “Set Point” temperature of 46.3 °C (115.4 °F). It is a this point that the inlet valve is activated for the high pressure steam enters the pipe heat exchanger immersed in the tank, so that sufficient thermal energy is sent to the tank water to prevent the temperature falls below 46.1 °C (115 °F). It is the manner that the steam feed control system is started, where the opening and closing of the inlet valve is automatically controlled by an on-of control system, so the water temperature is kept within the range 46.3–46.5 °C (115.4–115.7 °F).

Mathematical modelling and numerical simulation

Zero-dimensional mathematical modelling.

To mathematically model the mango hot water process in an initial state of cooling, the following hypotheses were considered for the system in general:

System to be analysed:	Water in the tank;
System type:	Closed;
Boundaries:	Mangoes, heat exchanger, plastic crates, walls tank;
Dimension:	0-D (homogeneous system);
State:	Transient;
Working effects:	Negligible (Σ W = 0);
Viscous dissipation:	Negligible (ε = 0).

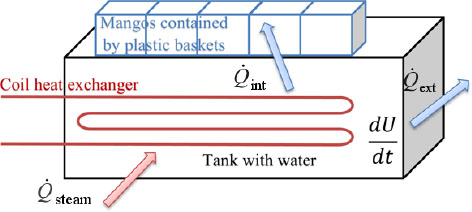
Having set the hypotheses for the mathematical model to be built, the energy interaction of the system under analysis with the boundaries is schematized in Figure 4. Starting from the first law of thermodynamics for a closed system that corresponds to the water in the tank, it has:

{\dot{Q}}_{steam} - {\dot{Q}}_{int} - {\dot{Q}}_{ext} = \frac{dU}{dt}

(1)

where ${\dot{Q}}_{steam}$ is the heat transfer rate from steam to tank water via pipe heat exchanger, ${\dot{Q}}_{int}$ is the heat transfer rate from tank water to the internal system composed by mangoes, plastic crates and the steel structure where the mango is driven. ${\dot{Q}}_{ext}$ is the heat transfer rate that is lost as a result of the system interaction with the environment, and dU/dt is the time variation of tank water thermal energy. It is worth pointing out that the working and viscous dissipation effects were neglected in order to simplifying the mathematical model.

Figure 4.

System schematic representation used for the 0-D mathematical modelling

Assuming that the properties of the water in a liquid state present not significant variation, it obtains:

\frac{{dT}_{water}}{dt} = \frac{1}{V_{water} ρ_{water} c_{p, water}} ({\dot{Q}}_{steam} - {\dot{Q}}_{int} - {\dot{Q}}_{ext})

(2)

This indicates that the time variation of the tank water temperature is affected by its capacity to store thermal energy and by its thermal interaction through its boundaries. Regarding the first point, it can be seen that the water volume into the tank remains constant throughout the time of the hot-water treatment of the mango takes to complete.

In order to obtain ${\dot{Q}}_{steam}$ , Villar [14] developed a mathematical model to describe the maximum heat transfer rate of steam provides to the tank water by means of a pipe heat exchanger. This process is achieved by assuming the pipe heat exchanger is sufficiently long enough so that, all the thermal energy from the steam flowing through the pipe heat exchanger is transferred to the water in the tank:

{\dot{Q}}_{steam} = {\dot{m}}_{steam} [H_{fg} + 0.68 c_{p, water} (T_{sat} - T_{water}) + c_{p, steam} (T_{steam} - T_{sat})

(3)

From the above equation, it is perceived that the heat transfer rate from steam to tank water, ${\dot{Q}}_{steam}$ , depends on the water temperature T_water(t), and thus of time, t. However, this dependency is weak since the variation in the water temperature during the transitional process of mango hot-water treatment is very small, and its contribution to the time variation of ${\dot{Q}}_{steam}$ is even smaller.

For the calculation of heat transfer rate from tank water to the internal system (mangoes, plastic baskets and steel structure), ${\dot{Q}}_{int}$ , it is necessary to specify, a priori, the most representative transient heat transfer approach. This procedure must be done because, it will be possible to characterize with a good precision the transient behavior of the heating of mangoes, and consequently, a good estimation of the tank water cooling curve can be achieved.

Because mangoes used in the hot-water treatment has the greatest thermal capacitance when is compare to plastic baskets and the steel structure, the calculation of ${\dot{Q}}_{int}$ will be represented by only the heat transfer rate from tank water to mangoes ${\dot{Q}}_{mango}$ multiplied by a factor that compensate this approach in terms of their thermal capacitances, i.e., ${\dot{Q}}_{int} = φ {\dot{Q}}_{mango}$ , where φ is a factor that relates the thermal capacitance of the internal system with respect to thermal capacitance of mangoes.

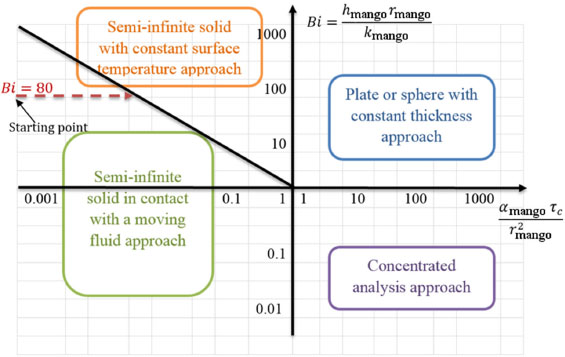
In order to determine ${\dot{Q}}_{mango}$ , it will be necessary to estimate the Biot number, Bi, and the Fourier number, $F o = α_{mango} τ_{c} / r_{mango}^{2}$ By doing this, the transient conduction model that best describes the mango heating process can be established.

Values of 360 min and 80 were found by the respective Fo and Bi. In accordance with Figure 5, the semi-infinite solid in contact with a moving fluid is the approach that best describes the initial heating of the mango [15]. Therefore, the heat transfer rate from tank water to the internal system (mangoes, plastic crates and steel structure) is estimated taking into consideration the aforementioned approach:

{\dot{Q}}_{int} = φ {\dot{Q}}_{mango} = φ N A_{1, mango} h (T_{agua} - T_{0, mango}) \exp (\frac{h^{2} α_{mango} t}{k_{mango}^{2}}) erfc [\frac{h}{k_{mango}} {(α_{mango} t)}^{1 / 2}]

(4)

This equation is based on the one formulated by Carslaw and Jaeger [16] for finding the temperature profiles of a semi-infinite solid in contact with a moving fluid.

Figure 5.

Domains of validations for several transient conduction approaches [15]

Finally, Villar [14], using empirical formulas of Churchill and Chu [17] demonstrated that the heat transfer rate transferred to the environment through the tank, ${\dot{Q}}_{ext}$ , is insignificant when is compared to the heat transfer rate from tank water to the internal system (mangoes, plastic crates and steel structures), ${\dot{Q}}_{int}$ So:

{\dot{Q}}_{ext} \approx 0

(5)

This is due to the tank walls are externally coated by a thermally insulating material (expanded polystyrene).

Substituting eqs. (3-5) in eq. (2) gives:

\frac{{dT}_{water}}{dt} = \frac{1}{V_{water} ρ_{water} c_{p, water}} {{\dot{m}}_{steam} [h_{fg} + 0.68 c_{p, water} (T_{sat} - T_{steam}) + c_{p, steam} (T_{steam} - T_{sat})] - φ N A_{1, mango} h (T_{0, mango} - T_{water}) \exp (\frac{h^{2} α_{mango} t}{k_{mango}^{2}}) erfc [\frac{h}{k_{mango}} {(α_{mango} t)}^{1 / 2}]}

(6)

This mathematical formulation correspond to an first order ordinary differential equation of type dT_water/dt = f(t, T_water), with initial value T_water(t = 0) = T_0,water, which predicts the transient cooling of tank water when hot-water treatment is initiated.

CFD modelling.

For the case of the vapour water submitted to condensation and considering homogeneous multiphase flow hypothesis in the water saturation region, the transport equations governing the turbulent, stationary, compressible and subsonic flow are described, under the Reynolds Average Navier Stokes (RANS) context, through the following mathematical formulas expressed in index notation:

\frac{\partial \bar{ρ}}{\partial t} + \frac{\partial \bar{ρ} {\tilde{u}}_{j}}{\partial x_{j}} = 0

(7)

\frac{\partial \bar{ρ} {\tilde{u}}_{l}}{\partial t} + \frac{\partial \bar{ρ} {\tilde{u}}_{j} {\tilde{u}}_{l}}{\partial x_{j}} = - \frac{\partial \bar{ρ}}{\partial x_{i}} + \bar{ρ} g_{i} + \frac{\partial}{\partial x_{j}} [μ (\frac{\partial {\tilde{u}}_{i}}{\partial x_{j}} + \frac{\partial {\tilde{u}}_{j}}{\partial x_{i}}) - \frac{2}{3} μ (\frac{\partial {\tilde{u}}_{k}}{\partial x_{k}}) δ_{i j}] + \frac{\partial (- \bar{ρ u_{l} ″ ​ u_{j} ″ ​})}{\partial x_{j}}

(8)

\frac{\partial \bar{ρ} {\tilde{H}}_{t}}{\partial t} + \frac{\partial \bar{ρ} {\tilde{u}}_{j} {\tilde{H}}_{t}}{\partial x_{j}} = \frac{\partial}{\partial x_{j}} [\frac{μ}{Pr} (\frac{\partial {\tilde{H}}_{t}}{\partial x_{j}})] + \frac{\partial (- \bar{ρ u_{j} ″ ​ H_{t} ″ ​})}{\partial x_{j}}

(9)

which, in differential form, eqs. (7-9) represent the conservation equations of mass (or continuity), linear momentum and energy (in the form of total enthalpy, ${\tilde{H}}_{t}$ ). From the above equations, terms such as $\bar{B}$ correspond to the time average of B also called as Reynolds average, while terms such as $\tilde{B}$ represent a density weighted average of B also called as Favre average. In the above equations, there are two open terms that need to be modelled:

The Reynolds stresses tensor, $- \bar{ρ u_{l} ″ u_{j} ″ }$ ;
The Reynolds heat flux, $- \bar{ρ u_{l} ″ H_{t} ″ }$ .

The Boussinesq hypothesis is commonly applied for the closure of the Reynolds stress tensor:

- \bar{ρ u_{l}' u_{j}'} = μ_{t} (\frac{\partial {\tilde{u}}_{i}}{\partial x_{j}} + \frac{\partial {\tilde{u}}_{j}}{\partial x_{i}}) - \frac{2}{3} μ_{t} (\frac{\partial {\bar{u}}_{k}}{\partial x_{k}}) δ_{ij} - \frac{2}{3} ρ κ δ_{ij}

(10)

where:

\bar{ρ} κ = \frac{1}{2} \bar{ρ u_{l} ″ ​ u_{l} ″ ​} = \frac{1}{2} (\bar{ρ {u ″}^{2}} + \bar{ρ {v ″}^{2}} + \bar{ρ {w ″}^{2}})

(11)

From the eqs. (10, 11), μ_t is the eddy viscosity, whereas κ is the turbulent kinetic energy. Moreover, u″, v″ and w″ are the velocity fluctuation aligned with their respective x, y and z, Cartesian directions. For the Reynolds heat flux, the gradient hypothesis is usually applied:

- \bar{ρ u_{j} ″ ​ H_{t} ″ ​} = \frac{μ_{t}}{σ_{h}} \frac{\partial {\tilde{H}}_{t}}{\partial x_{j}}

(12)

where σ_h is the turbulent Prandtl number whose assumed value is 0.9.

In order to find the turbulent viscosity, it is recommended, for compressible rotationally flows, the use of more sophisticated models for than the standard k-ε turbulent model. Therefore, the Wilcox k-ω turbulence model [18] will be used in this work, which is succinctly described by the following formulas:

\frac{\partial \bar{ρ} κ}{\partial t} + \frac{\partial \bar{ρ} {\tilde{u}}_{j} κ}{\partial x_{j}} = \frac{\partial}{\partial x_{j}} [(μ + \frac{μ_{t}}{σ_{κ}}) \frac{\partial κ}{\partial x_{j}}] + P_{κ} - Y_{κ}

(13)

\frac{\partial \bar{ρ} ω}{\partial t} + \frac{\partial \bar{ρ} {\tilde{u}}_{j} ω}{\partial x_{j}} = \frac{\partial}{\partial x_{j}} [(μ + \frac{μ_{t}}{σ_{ω}}) \frac{\partial ω}{\partial x_{j}}] + G_{ω} - Y_{ω}

(14)

μ_{t} = \frac{\bar{ρ} κ}{\overset{⌢}{ω}}

(15)

where:

\overset{⌢}{ω} = max (ω, C_{lim} \sqrt{\frac{2 {\tilde{S}}_{ij} {\tilde{S}}_{ij}}{β^{*}}})

(16)

In eqs. (13, 14), P_K and G_ω are the production of turbulent kinetic energy and the turbulent frequency, respectively, Y_K and Υ_ω indicate the destruction of turbulent kinetic energy and turbulent frequency, respectively. Prandtl numbers of turbulent kinetic energy, σ_κ, and turbulent frequency, σ_ω, are both assumed to be equal to 2. In the eq. (16), $\overset{⌢}{ω}$ is the corrected turbulence frequency, ${\tilde{S}}_{ij}$ is the Favre averaged strain rate tensor and β* is an additional calibration parameter of the Wilcox k-ω model itself [18].

For the case of the superheated steam flowing into the pipe-type heat exchanger, this pure substance transfers thermal energy to the tank water through the heat exchanger walls, which means the superheated steam temperature is reduced until it reaches the saturation temperature, T_s. At this temperature, a progressive transfer of thermal energy becomes apparent through the phase change, i.e. the formation of condensed water, until all the saturated steam has been totally transformed into condensed water, and then, an additional transfer of heat energy leads to this condensed water to drop in temperature until reaches values that are close to those of the liquid tank water.

The homogeneous multiphase flow hypothesis establishes that in the region where there is evidence of a biphasic mixture (i.e. saturated liquid and saturated steam), both phases share the same velocity, energy and turbulence field. That is, the homogeneous model assumes that the loads transported (except the mass fraction, Ỹ_l) are the same for all the phases.

This is why, if the homogeneous multiphase flow is taken by hypothesis, the transport equations described up to now are also valid for the internal region of the pipe-type heat exchanger, where, in some part of the system, the steam in a state of saturation will be gradually condensed as a result of a continuous thermal energy transfer to the tank water.

The equilibrium phase change model will be used in order to describe the condensation of steam. This model assumes that in the saturation region, both phases (liquid and steam) share the same temperature and the phase change occurs almost instantly in a way that this is found directly from the phase diagram. Therefore, the steam mass fraction, Ỹ_v, also known as quality, x, is calculated by:

x = {\tilde{Y}}_{v} = \frac{H_{m} - H_{l}}{H_{v} - H_{l}}

(17)

where H_m is the mean enthalpy of the mixture in the biphasic saturated region of water which is calculated by taking the transfer equation of energy, ${\tilde{H}}_{t}$ , while H_l and H_vcorrespond for a given pressure, to the enthalpies of the saturated liquid and the saturated vapour. Generally speaking, this is true inside the saturated region, 0 < $0 \leq {\tilde{Y}}_{v} \leq 1$ :

B_{m} = (1 - {\tilde{Y}}_{v}) B_{l} + Y_{v} B_{v}

(18)

where B_m is any property of the fluid mixture such as entropy, enthalpy, specific heat, heat conductivity or dynamic viscosity. For the mixture density in the saturation region:

\frac{1}{\bar{ρ}} = \frac{1 - {\tilde{Y}}_{v}}{{\bar{ρ}}_{l}} + \frac{{\tilde{Y}}_{v}}{{\bar{ρ}}_{v}}

(19)

which is equivalent to v = (1 − x)v_l + xv_v. It should be pointed out that when Ỹ_v > 1, the mixture is 100% superheated steam, and so, must be considered as properties those characteristics of steam. Likewise, for Ỹ_v < 0, the mixture is a 100% supercooled liquid, and therefore only the properties of water in a liquid state should be taken into account.

Numerical simulations setup

Computational fluid dynamics simulation in transient state.

A prior CFD simulation in transient state is made in order to determine the time evolution of the convective heat transfer coefficient between the water and the surface of mangoes contained in the plastic crates, h, in order to solve the zero-dimensional model, i.e., eq. (6). Moreover, the transient behaviour of mangoes temperature piled in a plastic crate, ${\bar{T}}_{mango}$ , is also determined for the purpose of analysing the mean heating rate from the water to the mangos.

In this simulation, a previously experimentally determined 80 mm/s of uniform flow of water with 47.5 °C (117.5 °F) pass through the plastic crate that are filled with 23 same sized spheroidal mangoes (9 and 11 cm for minor and major axes, respectively). The mangos’ initial temperature is 21.1 °C (69.8 °F) in all of their domain, which was considered as homogeneous entities, i.e., without the presence of the core. The mango’s transport properties are assumed as constants and taken from the work of Bon et al. [19].

The numerical simulation was made through the use of Ansys-CFX^TM commercial software. A Supermicro^TM WorkStation with E5-2670 v2 Intel^TM Xeon^TM processor (25M Cache, 2.50 GHz) and 32 Gb of RAM memory are used for the transient simulation. The processing time for this case was 48 h, approximately.

Numerical simulation of the zero-dimensional model.

The numerical solution of eq. (6) is carried out using the 4^th order Runge-Kutta method. It should be noted that thermodynamics and transfer properties of mango and tank water must be known prior to resolve that equation. The mango properties were taken into account as being equal to those found from the experimental work of Bon et al. [19].

In addition, it is also necessary to know the convective heat transfer coefficient between the water and the mangoes piled in a plastic crate. This convective heat transfer coefficient depends of geometrical arrangement among tank water and mangos-crate system, as well as their fluidynamic and thermal interactions, and can be found by experimentation or through computational fluid dynamics techniques.

Computational fluid dynamics simulation in a steady state.

ANSYS-CFXTM software was used as a simulation tool. In this way 16 and 23 million of hexahedral and tetrahedral elements were used to discretize the computational domains of the “Original” and “Hybrid” equipments. For numerical solving, the conservation equations involved in the fluid-dynamic and thermal processes of the equipment under operation were spatially discretized using a first order upwind differencing scheme. The following criteria were considered to meet convergence:

RMS residuals have set to be less than 10⁻⁴;
Transport equations imbalances must be less than 0.1%.

Both simulations were conducted using parallel processing on a Supermicro^TMWorkStation with a E5-2670 v2 Intel^TM Xeon^TM processor (25M Cache, 2.50 GHz) and 32 Gb of RAM memory. The computational time required to obtain the results were approximately 350 and 480 hours for the “Original” and “Hybrid” cases, respectively.

RESULTS AND DISCUSSIONS

Determination of convective heat transfer between mangos and tank water

Figure 6 shows a set of images reflecting the temperature gradients for the times of 1, 5, 15 and 25 min after the mangoes at an initial temperature of 21.1 °C (69.8 °F), have been exposed to a uniform flow of water at 80 mm/s and 47.5 °C (117.5 °F). These input values have been verified under the conditions in which the “Original” equipment begins the hot-water treatment of the mango.

Figure 6.

Time-evolution of mango temperature

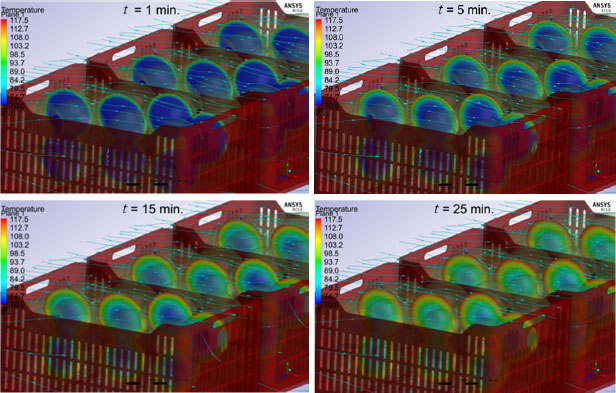
Note that in Figure 6, in spite of the first 25 min having passed, the mangoes have still not reached a homogeneous temperature. To the contrary, high temperature gradients can be seen inside them, which occur particularly in the regions near to the mango walls.

If it analyses the global quantitative parameters, Figure 7 shows that the mango undergoes a high increase in mean temperature at the beginning of the hot water treatment. However, as the time passes, this increase tends to fall. Apart from this, it can be seen that 25 min after starting the hot-water treatment, the mean temperature of the mango has risen by approximately 17 °C (30.6 °F), reaching a mean temperature of around 38 °C (100.4 °F).

Figure 7.

Time evolution of: the mango mean temperature and, the convective heat transfer coefficient of the mango-plastic crate system

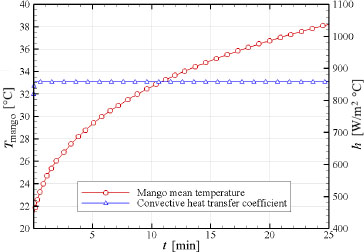
Likewise, Figure 7 shows the mean convective heat transfer coefficient of tank hot water that flows over a pile of mangoes and the plastic crate. It is noted that, in the first second of the hot-water treatment, the convective heat transfer coefficient is 820 W/m² K. Then, it rises in the first 4 seconds until it reaches 857 W/m² K, value that remains constant during the whole time of the treatment. This initial behaviour is due to the dynamic response that numerically occurs in a manner that external steady state convective heat transfer boundary conditions is coupling with the internal transient conduction heat transfer.

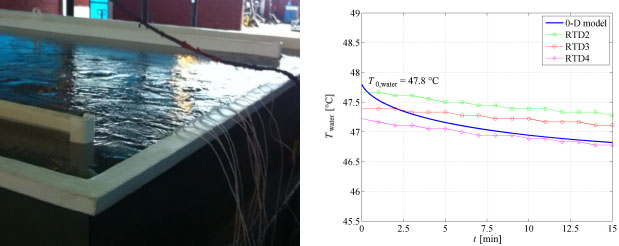
Validation of the 0-D model through field measurements of the “Original” equipment

By taking the results of the heat transfer convective coefficient calculated by CFD simulation, the transient behaviour of the tank water temperature can be found for the whole time of the hot-water treatment of mango. Figure 8 illustrates the time variation of the tank water temperature in the initial stages of the hot-water treatment of 3.5 Tons of mango using the “Original” equipment (filled with 19 m³ of liquid water).

Figure 8.

Field measurements and 0-D mathematical model results of the tank water temperature in the initial stage of the “Original” mango hot-water treatment equipment

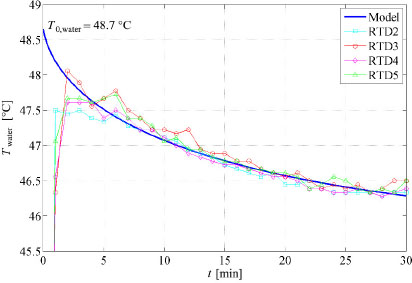
It shows that, under the hypothesis of an initial water temperature of 48.7 °C (119.6 °F) and a continuous injection of steam of 20 g/s (at 1 atm and 150 °C), the 0-D mathematical model reflects the results obtained in the field studies with an excellent approximation. In particular, it can be seen how the curve generated by the 0-D mathematical model in most of the domain is within the range of temperatures measured by the RTDs 2, 3, 4 and 5 which were located at different spatial points “downstream” the principal region of the tank.

It should be pointed out that during the first minute after beginning the hot water treatment the field results show scattered values but less than those found from the 0-D model. This disparity is to be expected, since, in a real situation, there is a time-out where a large mass of hot water flows from “upstream” ( t = 0 min) to “downstream” (t > 0 min), the last, where the RTDs 2, 3, 4 and 5 are placed. An order-of-magnitude analysis carried out on the “Original” equipment found that the time-out is approximately 1.33 min.

In this way, the 0-D mathematical model was validated against field measurements that were obtained in the operation of the “Original” equipment. Once the model can predict the global thermal state of the water at any instant in time during the hot-water treatment, it can be used as a mathematical tool in order to predict the global thermal behaviour of the water in any hot-water treatment equipment. This model is therefore capable of representing the transient behaviour of the tank water temperature according to three input parameters:

The volume of tank water, V_water;
The steam flow that enters the pipe-type heat exchanger, ṁ_steam;
The initial temperature of the water, T_0,water.

These parameters are fundamental for the design of any mango hot-water treatment equipment.

Basic design of the hybrid equipment

The 0-D mathematical model will thus be used as a tool in order to design new equipment that will be referred as “Hybrid” equipment, and which must simultaneously comply with the export protocols required by the USA and Japan.

In the specific case of exporting mangoes to Japan, the regulations state that a hot-water treatment is only successfully carried out if the transient temperature of the tank water is within a narrow margin of tenth of Fahrenheit degrees. That is, the initial temperature must not exceed 47 °C (116.6 °F), and the temperature during the first 5 minutes after beginning the treatment must not be less than 46.3 °C (115.3 °F). Therefore, if the 0-D mathematical model is used, the tank water volume and the initial steam mass flow can be estimated. The determination of both parameters must ensure that the water temperature drop to be less than 1 °F during the first 5 minutes of the hot-water treatment.

In accordance with the restrictions imposed by Japan, i.e. T_0,water = 47 °C (116.6 °F), a continuous injection of steam of 30 g/s is required in the pipe heat exchanger. The graph in Figure 9 shows the transient behaviour of the tank water for capacity of 19, 25 and 30 m³ of such substance. It can be seen that for a 19 m³ of tank water (which is characteristic of the “Original” equipment), the initial mango hot-water treatment process will exhibit a sudden drop in the water temperature in just the first 2 minutes, which exceeds the minimum admissible temperature imposed by Japan regulations for mango exports.

Figure 9.

Evolution of the tank water temperature over time, obtained from different volumes of water and for a steam feed of 30 g/s

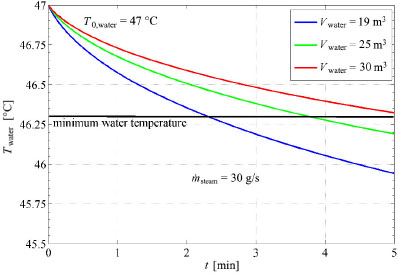
For a 25 m³ capacity water tank, the cooling process is a little slower. However, before the first 4 minutes have passed, the water temperature will have dropped below the minimum temperature required by the Japanese standard 46.3 °C (115.3 °F). A tank that can store over 30 m³ of water still complies with the Japanese requirement, which states that the initial tank water temperature must be 47 °C (116.6 °F) and must not drop by more than 0.6 °C (1.1 °F) after the first 5 minutes after the mango hot-water treatment has been started.

Therefore, for the hot-water treatment of 3.5 tons of mango, if the “Hybrid” equipment is to comply with Japanese regulations, it must possess the following design parameters:

A tank that will ensure a minimum of 30 m³ of liquid water;
A continuous feeding of at least 30 g/s of superheated steam at 150 °C and 1 atm.

It must be emphasized that since the Japanese regulations are much more stringent compared to the American ones, a hot water treatment equipment design that meets the Japan requirements also meets the technical requirements imposed by the USA. This last statement is based on the results of the transient tank water temperature analysis of the “Hybrid” equipment that took account of the American regulations. However, these will not be presented in this work for the sake of brevity.

Brief description of the complementary design of the “Hybrid” equipment

After identifying the main geometric and operational parameters of the “Hybrid” equipment, these were applied to the design of a new geometric configuration.

Figure 10 shows the 3-D geometry of the “Hybrid” equipment that was designed taking into account the aforementioned results obtained by the use of the 0-D mathematical model. As can be appreciated, the “Hybrid” equipment comprises a tank whose geometric volume is 52% greater than the “Original” equipment.

Figure 10.

3-D geometry of the designed “Hybrid” equipment

It can also be seen that the “Hybrid” equipment has two heating channels. Each channel has two “marine-type propellers” and two pipe-type heat exchangers, each of these heat exchanger is compressed by 16 rows of ϕ 1” Sch 40 pipes, designed so that the steam input flow is divided into two parallel lines with the steam flowing through 8 rows of ϕ1” pipe.

Fluid dynamic and thermal performance of the “Hybrid” equipment through CFD analysis

Subsequently, both pieces of mango hot water treatment equipment (“Original” and “Hybrid”), were simulated using the CFD in order to make qualitative and quantitative comparisons of the fluid-dynamic and thermal behaviour of both pieces of equipment when subjected to the same operating conditions; that is a steady state regime and with no mangoes inside the tank.

In order to compare the fluid-dynamic and thermal performance, the operating conditions were set for both tanks:

A steam feed to the pipe-type heat exchanger of 20 g/s at 150 °C and 1 atm;
“Marine-type propellers” (2 propellers in the “Original” and 4 propellers in the “Hybrid”) that rotate at a speed of 770 rpm.

By means of a qualitative comparison of the fluid-dynamic performance of the “Original” and “Hybrid” equipments, Figure 11 depicts the streamlines coloured by the velocity magnitude. It can be seen that tank water velocities in the main region of the “Hybrid” equipment are higher than for those observed for the “Original” one. Regarding the flow pattern, it can be seen that the “Hybrid” equipment adopts a type-symmetric one. Both enhancements observed by the “Hybrid” equipment result in a higher spatial and temporal homogeneity of the tank water temperature, which leads to a better heat interaction between the tank water and the mangoes.

Figure 11.

Plant view of 3-D streamlines of tank-water flowing in the “Hybrid” (top) and “Original” (bottom) equipments

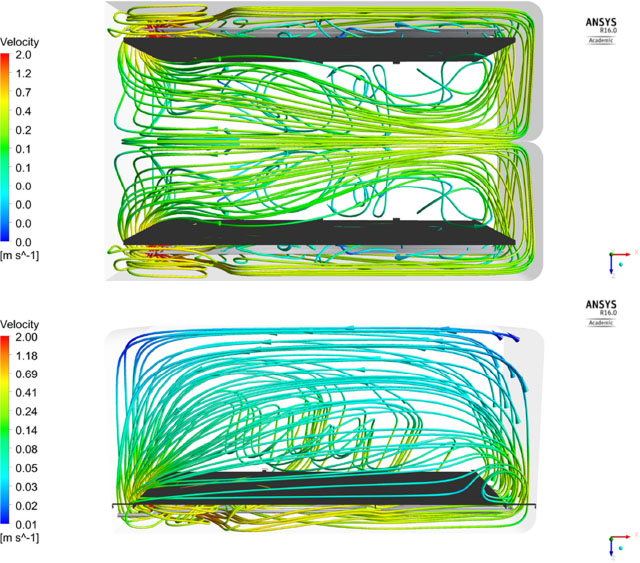
Table 1 lists the main global parameters that describe the thermal behaviour of the pipe-type heat exchanger corresponding to “Original” and “Hybrid” equipments. It can be seen that for the same input condition, (20 g/s of steam at 150 °C and 1 atm), the heat transfer rate that is transmitted to the tank water by the steam, -math-, in the case of the “Hybrid” equipment is 9% more than that transmitted by the “Original” equipment. This is to be expected since the two ϕ 1” pipe lines of the “Hybrid” equipment have an almost 30% greater surface area compared to the single line of ϕ 2” pipes of the “Original” equipment. It should be pointed out that the “Original” equipment does not make maximum use of the heat energy of the steam, a reason why the water is still in a liquid saturated state at the water outlet.

Table 1.

Global parameters obtained from the pipe-type heat exchanger of “Original” and “Hybrid” equipments

Parameters	Original	Hybrid
ṁ_liq,out	19.999 g/s	20 g/s
ṁ_vap,out	0.001 g/s	0 g/s
${\tilde{T}}_{out}$	99.7 °C	48.7 °C
H_in − H_out	2,364 kJ/kg	2,576 kJ/kg
${\dot{Q}}_{steam}$	47.3 kW	51.5 kW
A_wall	8.76 m²	11.34 m²
q^″_p	5,399 W/m²	4,543 W/m²

The previously discussed in Table 1 is also observed in Figure 12. As can be seen for the “Hybrid” equipment, the mean temperature of water that exits the ϕ 1” pipe heat exchanger (equal to 48.7 °C) is practically the same as the temperature of the tank water (equal to 47.5 °C). The opposite of what is seen for the “Original” equipment where, the mean water temperature at the outlet of ϕ 2” pipe heat exchanger is the same as the water saturation temperature (equal to 99.7 °C), which is 50 °C higher than the tank temperature. It gives an increase of 9% of the thermal power transferred to the tank water.

Figure 12.

Temperature field of the water inside the pipe-type heat exchanger for the “Hybrid” (left) and “Original” (right) equipments

Validation of the 0-D model through field measurements of the “Hybrid” equipment

Finally, the thermal performance of the built “Hybrid” equipment is validates in a similar manner that those made for the “Original” ones, i.e., several Pt-100 type RTDs was placed at different positions of the tank in order to record the transient behaviour.

As can be shown in Figure 13, the acquired tank water temperatures exhibit the same slope as previously predicted by the 0-D mathematical model. Once again, it is demonstrated the validity of the 0-D mathematical model for design purposes of hot-water treatment equipments.

Figure 13.

Data acquisition results of the “Hybrid” equipment during mango’s hot-water treatment

CONCLUSIONS

A mathematical 0-D model has been developed in this work in order to describe the transient state of the tank water temperature in mango hot-water treatment equipments. The application of this model permitted to identify the main geometric and operating parameters that involves in the thermal behaviour of the tank water in the initial phase of the treatment. In this way, new hot-water treatment equipment called as “Hybrid” was designed in order to simultaneously satisfy the phytosanitary requirements of the USA and Japan for the mangoes exportation.

Then, the CFD was applied to study with a high level of sophistication and detail, the fluid-dynamic and thermal behaviour of “Original” and “Hybrid” equipments. CFD results confirmed that the “Hybrid” equipment has a better thermal performance than the “Original” equipment since the thermal power transferred to the tank water increased by 9%.

In this way, it is evidenced the usefulness of CFD as a numerical-computational tool for the analysis and design of process equipments. Because that way, a wide range of full scale quantitative and qualitative results can be obtained under real operating conditions and at a relatively low cost compared to setting up experimental test benches.

NOMENCLATURE

A_1,mango	external area of one mango that involves in the hot-water treatment	[m²]
A_wall	internal area of a pipe-type heat exchanger walls	[m²]
B	any quantity or property	[-]
B_l	property of a substance at saturated liquid condition	[-]
B_v	property of a substance at saturated vapor condition	[-]
B_i	biot number	[-]
C_p,steam	constant pressure specific heat of steam at a given pressure	[kJ/kg K]
C_p,water	constant pressure specific heat of tank water	[kJ/kg K]
G_ω	production term of turbulent frequency	[kg/m³ s²]
h	convective heat transfer coefficient between water and mangoes	[W/m K]
H_l	enthalpy of saturated liquid water at a given pressure	[kJ/kg]
H_lv	enthalpy of vaporization of steam at a given pressure	[kJ/kg]
H_t	total enthalpy	[kJ/kg]
H_in	enthalpy of steam at the entrance of the pipe heat exchanger	[kJ/kg]
H_out	enthalpy of water at the exit of the pipe heat exchanger	[kJ/kg]
H_v	enthalpy of saturated vapour water at a given pressure	[kJ/kg]
H_m	enthalpy of the mixture in the saturated region of water	[kJ/kg]
k_mango	thermal conductivity of mango	[W/m² K]
L	length of the tank	[m]
ṁ_l_iq,out	mass flow of condensed water that exits from the heat exchanger	[kg/s]
ṁ_steam	mass flow of steam that enters to the heat exchanger	[kg/s]
ṁ_vap,out	mass flow of saturated vapour that exits from the heat exchanger	[kg/s]
N	total number of mangoes involved in the hot-water treatment	[-]
p	static pressure	[Pa]
p_K	production term of turbulent energy kinetic	[kg/m s]
q_p″	wall heat flux through pipe heat exchanger walls	[W/m²]
${\dot{Q}}_{steam}$	heat transfer rate from steam to tank water	[W]
${\dot{Q}}_{ext}$	heat transfer rate from tank water to environment	[W]
${\dot{Q}}_{int}$	heat transfer rate from tank water to the internal system	[W]
${\dot{Q}}_{mango}$	heat transfer rate from tank water to mangoes	[W]
r_mango	mango representative radius	[m]
${\tilde{S}}_{i j}$	favre-averaged strain rate tensor	[1/s]
t	time	[s]
T_sat	water saturation temperature at a given pressure	[K]
${\bar{T}}_{mango}$	mean temperature of mangoes piled in a plastic crate	[K]
${\tilde{T}}_{out}$	mass flow averaged temperature of water that exits the heat exchanger	[K]
T_steam	steam temperature	[K]
T_water	tank water temperature	[K]
T_0,water	tank water temperature at 0 s	[K]
u_i	instantaneous velocity vector	[m/s]
ũ_i	favre-averaged velocity vector	[m/s]
u_i″	favre fluctuating velocity vector	[m/s]
U	internal energy of tank water	[kJ]
V_water	tank water volume	[m³]
W	mechanical work	[kJ]
x	vapor quality	[-]
x_i	position vector	[m]
Ỹ_v	favre-averaged of steam mass fraction	[-]
Y_K	destruction term of turbulent energy kinetic	[kg/m s]
Υ_ω	destruction term of turbulent frequency	[kg/m³ s²]

Greek letters

α_mango	thermal diffusivity of mango	[m²/s]
ß^*	an additional calibration parameter of the Wilcox k-ω model	[-]
δ_ij	kronecker delta	[-]
ε	viscous dissipation	[m²/s³]
κ	turbulent kinetic energy	[m²/s²]
μ	molecular viscosity	[Pa s]
μ_t	eddy viscosity	[Pa s]
V	specific volume of water	[kg/m³]
v_l	specific volume of saturated liquid water at a given pressure	[m³/kg]
ν_ν	specific volume of saturated vapor water at a given pressure	[m³/kg]
$\bar{ρ}$	reynolds-averaged density	[kg/m³]
${\bar{ρ}}_{l}$	density of saturated liquid water at a given pressure	[kg/m³]
${\bar{ρ}}_{v}$	density of saturated vapour water at a given pressure	[kg/m³]
ρ_water	tank water density	[kg/m³]
σ_h	turbulent Prandtl number	[-]
σ_κ	turbulent kinetic energy Prandtl number	[-]
σ_ω	eddy dissipation Prandtl number	[-]
τ_c	transition time	[s]
φ	thermal capacitance rate between internal system and mangoes	[-]
ω	turbulence frequency	[1/s]
$\overset{⌢}{ω}$	corrected turbulence frequency	[1/s]

REFERENCES

Ridoutt B., Juliano P., Sanguanri P., Sellahewa J., The Water Footprint of Food Waste: Case Study of Fresh Mango in Australia, Journal of Cleaner Production, Vol. Vol. 18 (No. 16-17), :1714-17212010
FAO Statistical Database, 1999, Agriculture, Food and Cultural Production Yearbook, Food and Agricultural Organization of the United Nations
Torres R., Economic Analysis of Climate Change in Agriculture in the Piura-Peru Region: Main Agroexport Products (in Spanish), 2010
Fossa V., Successful Experience of Mango Producers in Piura-Peru (in Spanish), Final Report, Don Humberto Fund, 2013
Sharp J., Picho-Martinez H., Hot Water Quarantine Treatment to Control Fruit Flies in Mangoes Imported into the United States from Peru, Journal of Economic Entomology, Vol. Vol. 83 (No. 5), :1940-19431990
Jacobi K., Wong L., Quality of “Kensington” Mango (Mangifera Indica Linn.) following Hot Water and Vapour-heat Treatments, Postharvest Biology and Technology, Vol. Vol. 1 , :349-3591992
Jacobi K., RacRae E., Hetherington S., Postharvest Heat Disinfection Treatments of Mango Fruits, Scientia Horticulturae, Vol. Vol. 89 , :171-1932001
USDA, SENASA y APEM, Work Plan for the Peruvian Mango Treatment and Preclearance Program, Lima-Peru, 2010
Nascimento A., Malavasi A., Morgante J., Duarte A., Hot-Water Immersion Treatment for Mangoes Infested with Anastrepha Fraterculus, A. Obliqua, and Ceratitis Capitata (Diptera: Tephritidae) in Brazil, Journal of Economic Entomology, Vol. Vol. 85 (No. 2), :456-4601992
Wang S., Tang J., Cavaliery R., Modelling Fruit Internal Heating Rates for Hot Air and Hot Water Treatments, Postharvest Biology and Technology, Vol. Vol. 22 (No. 3), :257-2702001
Rezagah M., Ishida S., Tanaka F., Hamanaka D., Uchino T., Three-dimensional Heat Transfer Modeling in Japanese Pears (Pyrus pyrifolia) during Tempering, Food Science and Technology Research, Vol. Vol. 19 (No. 5), :765-7712013
Valle-Guadarrama S., Hemández-Álvarez R., Civarrubias-Gutiérrez I., Modelling of the Heating and Cooling Internal Rates in Fruits, Case: Mexican Lime, Revista Fitotecnia Mexicana, Vol. Vol. 30 , :61-682007
Malca V., State of the Art of Mango Hydrothermal Treatment in Peru (in Spanish), 2014
Villar Y., Generalities of the Hydrothermal Mango Treatment in Peru (in Spanish), 2014
Bejan A., Heat Transfer (in Portuguese), Editorial Edgard Blucher Ltda, 1994
Carslaw H., Jaeger J., , Conduction of Heat in Solids, 1959
Churchill S., Chu H., Correlating Equations for Laminar and Turbulent Free Convection from a Vertical Plate, International Journal of Heat Mass Transfer, Vol. Vol. 18 (No. 11), :1323-13291975
Wilcox D., Formulation of the k-ω Turbulence Model Revisited, AIAA Journal, Vol. Vol. 46 (No. 2), :2823-28382008
Bon J., Váquiro H., Benedito J., Telis-Romero J., Thermophysical Properties of Mango Pulp (Mangifera Indica L. cv. Tommy Atkins), Journal of Food Engineering, Vol. Vol. 97 (No. 4), :563-5682010